今回は、PyTorchで線形回帰のサンプルコードを実装しながら、簡単な解説をしていきます。
また今回のプログラミングには、Pythonの知識が必要です。
Pythonについて基礎的なところから、効率的に学ぶなら、以下の記事がピッタリです。
今回の開発環境
開発環境の前提は以下の通り。
- PyTorchを使用
- 開発環境は、Google Colaboratory
- テストデータは乱数を使用して、自分で作成
Google Colaboratoryはブラウザで操作出来て、環境構築も不要です。GPUも制限はありますが、使えるのでオススメです。
コードの全体は、GitHubにアップロードしています。
線形回帰のデータ準備
まず必要なライブラリをインポートします。
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
plt.style.use("ggplot")そして、今回は乱数を使用しますので、以下を書きます。
# 乱数を使用した時に、毎回同じ結果を得るために指定
torch.manual_seed(123)そして、訓練データを作っていきます。
a = 5
b = 2
# 0〜10の間のデータを100個作成
x = torch.linspace(0, 10, 100)xの値を見てみると以下のようになります。
x
# 以下は出力値
tensor([ 0.0000, 0.1010, 0.2020, 0.3030, 0.4040, 0.5051, 0.6061, 0.7071,
0.8081, 0.9091, 1.0101, 1.1111, 1.2121, 1.3131, 1.4141, 1.5152,
1.6162, 1.7172, 1.8182, 1.9192, 2.0202, 2.1212, 2.2222, 2.3232,
2.4242, 2.5253, 2.6263, 2.7273, 2.8283, 2.9293, 3.0303, 3.1313,
3.2323, 3.3333, 3.4343, 3.5354, 3.6364, 3.7374, 3.8384, 3.9394,
4.0404, 4.1414, 4.2424, 4.3434, 4.4444, 4.5455, 4.6465, 4.7475,
4.8485, 4.9495, 5.0505, 5.1515, 5.2525, 5.3535, 5.4545, 5.5556,
5.6566, 5.7576, 5.8586, 5.9596, 6.0606, 6.1616, 6.2626, 6.3636,
6.4646, 6.5657, 6.6667, 6.7677, 6.8687, 6.9697, 7.0707, 7.1717,
7.2727, 7.3737, 7.4747, 7.5758, 7.6768, 7.7778, 7.8788, 7.9798,
8.0808, 8.1818, 8.2828, 8.3838, 8.4848, 8.5859, 8.6869, 8.7879,
8.8889, 8.9899, 9.0909, 9.1919, 9.2929, 9.3939, 9.4950, 9.5960,
9.6970, 9.7980, 9.8990, 10.0000])0〜10までの間でデータが入っていることが確認出来ると思います。
次にxのサイズ数を調整します。
# view:サイズ数を調整する。
# 第一引数はバッチの次元を指定する。
x = x.view(100, 1)すると、以下は元々1個の配列に100個データが入っていたが、100個の配列に1個のデータが入るように変形されます。
以下のような感じ。
x
# 以下は出力値
tensor([[ 0.0000],
[ 0.1010],
[ 0.2020],
(省略)
[ 9.6970],
[ 9.7980],
[ 9.8990],
[10.0000]])長くなるので、途中省略していますが、100個のデータが一つの配列に入っています。
そして、1次関数式を以下のように定義します。
eps = torch.randn(100, 1)
y = a * x + b + eps先程作った式を、matplotlibで散布図で描画します。
# 散布図を描画する。第1引数にx軸、第2引数にy軸を指定する。
plt.scatter(x, y)すると、以下のような図になります。
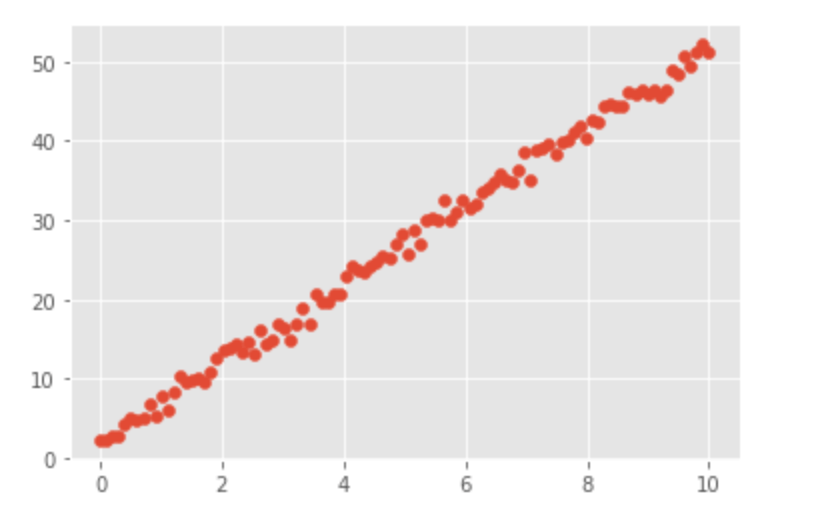
線形回帰のモデル実装
次に線形回帰のモデルを実装していきます。
class LR(nn.Module):
def __init__(self):
super().__init__()
# in_features:入力値の数、out_features:出力値の数
self.linear = nn.Linear(in_features=1, out_features=1)
# 順伝播、forwardを定義しておくと、学習中に自動的に呼ばれる
def forward(self, x):
output = self.linear(x)
return outputスーパークラスとして、「torch.nn」を継承し、初期化処理でスーパークラスの初期化、モデルの定義をしています。
今回は線形回帰と言うことで、nnから「Linear」モデルを使います。
nn.Linearの第1引数には入力値の数を指定し、第2引数には出力値の数を指定します。今回はどちらも1になります。
次に、forward関数を定義して、順伝播の処理内容を書きます。
第2引数には入力値であるxを渡します。今回はself.linear(x)が計算した結果をoutputとして返却しています。
ここで定義したforward関数は学習中にスーパークラスから自動的に呼び出されます。
そして定義したモデルを使えるようにmodel変数に代入をします。
model = LR()学習前の線形回帰モデルの性能を確認
学習前のモデルの性能を確認するために、x2というテストデータを作成して、そのデータをmodelに引数として渡して、y_predという予測値を得ます。
x2 = torch.linspace(0, 3, 100).view(100, 1)
y_pred = model(x2)
y_pred
# 以下は出力値
tensor([[ 1.1556e-01],
[ 9.2342e-02],
[ 6.9127e-02],
[ 4.5912e-02],
(省略)
[-2.1363e+00],
[-2.1595e+00],
[-2.1827e+00]], grad_fn=<AddmmBackward>)さて、ここで図を出力してみて、どれくらい予想が合っているのか確認をします。
そのために、予測値であるy_predを一本の線として出力し、正解データであるxとyを散布図として出力します。
# 順伝播をしているので、勾配計算処理を外す => detach()
# plot:一本の線を描画
plt.plot(x2, y_pred.detach(), label="prediction")
plt.scatter(x, y, label="data")
plt.legend()図を出力するために、勾配計算処理を外す「detach()」が必要なことに注意して下さい。
出力した図は以下のようになりました。
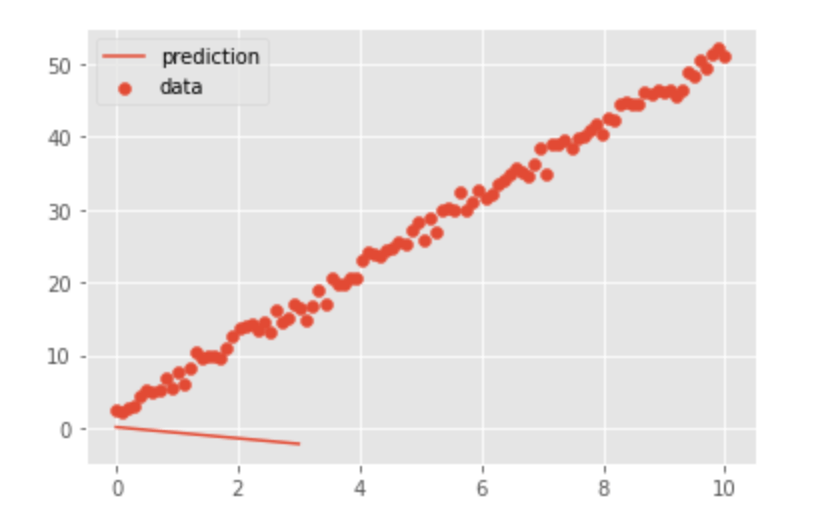
学習をしていないため、全く見当外れのところに予想されて線が引かれていることが分かると思います!
線形回帰モデルの学習
さて、ここからは線形回帰モデルを使って、実際にデータを学習させて行きたいと思います。
# 損失関数
criterion = nn.MSELoss()
# 最適化関数
# 第1引数:model.parameters() => 重みとバイアスの情報が入っている。これを更新したい。
# 第2引数:学習率
optimizer = optim.SGD(model.parameters(), lr=0.001)データを学習するために、以下のようにコードを書きます。
losses = []
num_epoch = 500
for epoch in range(num_epoch):
# ミニバッチのloopがないため、バッチ学習
# 勾配の初期化を行う
optimizer.zero_grad()
# 予測値の計算
y_pred = model(x)
# 損失の計算:予想値と正解値を与える
loss = criterion(y_pred, y)
# 損失を誤差逆伝播する
loss.backward()
# 重みとバイアスの更新
optimizer.step()
if epoch % 10 == 0:
print("epoch: {}, loss: {}".format(epoch, loss.item()))
losses.append(loss.item())すると、以下のような感じで学習が進むたびに、損失の値が小さくなっていることがわかります。
# 以下は出力値
epoch: 0, loss: 1221.19384765625
epoch: 10, loss: 296.3516540527344
epoch: 20, loss: 72.65264129638672
epoch: 30, loss: 18.543027877807617
epoch: 40, loss: 5.452998161315918
epoch: 50, loss: 2.284636974334717
epoch: 60, loss: 1.516102910041809
epoch: 70, loss: 1.328049898147583
epoch: 80, loss: 1.280423879623413
epoch: 90, loss: 1.2667850255966187
(省略)
epoch: 400, loss: 1.1888651847839355
epoch: 410, loss: 1.1868232488632202
epoch: 420, loss: 1.1848024129867554
epoch: 430, loss: 1.182801365852356
epoch: 440, loss: 1.180820107460022
epoch: 450, loss: 1.1788581609725952
epoch: 460, loss: 1.1769163608551025
epoch: 470, loss: 1.1749935150146484
epoch: 480, loss: 1.1730895042419434
epoch: 490, loss: 1.1712037324905396損失の経過を図にします。
plt.plot(losses)すると以下のような感じになります。
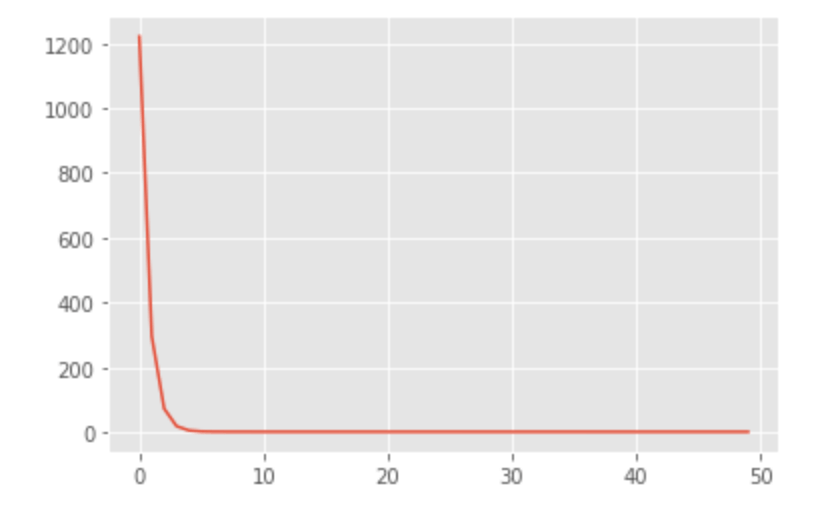
かなり早い段階から学習が収束しているのが分かります。
それでは、学習した結果、どれくらい予想値が合っているか図にして見てみましょう。
x_test = torch.linspace(0, 10, 100).view(100, 1)
y_test = model(x_test)
plt.plot(x_test, y_test.detach(), label="prediction")
plt.scatter(x, y, label="data")
plt.legend()図にした結果がこちらです。
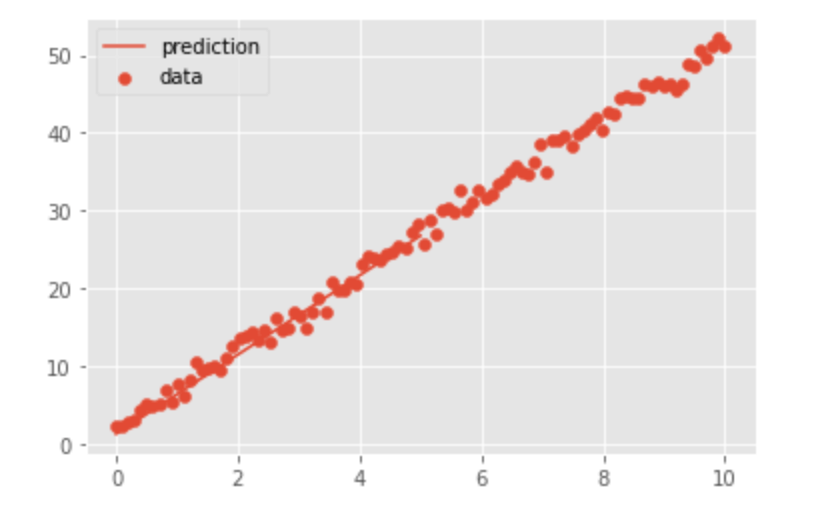
単純なデータなので当たり前ですが、かなりいい感じで線を引いてくれて、モデルの性能がかなり良いことが分かります。
最後に
今後も勉強の過程として、PyTorchを使ったDeep Learningのコードサンプルを記事にしたいと思っています。
ここまでお読みいただき、ありがとうございました。
\ 更新の励みになるので、ポチッとしてね /



他にもスキルアップやキャリアアップの役に立つ情報が満載です。他の記事も読んで、ゆっくりしていってね!
この続きは以下から。
ディープラーニングの数学的な知識を身に着けたいなら、以下。
ディープ・ラーニングを本気で学ぶなら、Udemyがおすすめ
- 学習コンテンツ量が多いので、未経験から現場で活躍するレベルまで幅広い
- 疲れていても、動画で楽に学習出来る
- 疑問を気軽に聞けるQAシステムがあり、初心者でも安心
- セールが多数開催されるので、Udemy
- 30日以内なら、返金も可能
まとめると、「動画で楽に勉強が出来て、質問も出来て、しかも安い」という点が、Udemy
エンジニアのスキルアップに終わりはありませんが、時代が進むにつれて、学習コストは低くなっています。技術書で独学するのに、限界を感じているのであれば、Udemy
Udemyをもっと知りたいなら


もちろん、ディープ・ラーニングに関する講座も豊富です。どんな講座があるかは、以下から確認して下さい。
\ 動画だから、挫折しにくい /
※30日以内なら、返金あり



コメント
コメント一覧 (1件)
[…] 関連記事 PyTorchで線形回帰を実装してみる […]